Binary Search

Image from GeeksForGeeks

#binary_search, #binary_chop, #half_interval_search, #logarithmic_search

Condition

• The data structure must be sorted
• Can access to any item in the data structure with a constant time

Time Complexity

Best case: O(1)
Average case: O(log n)
Worst case: O(log n)

Algorithm

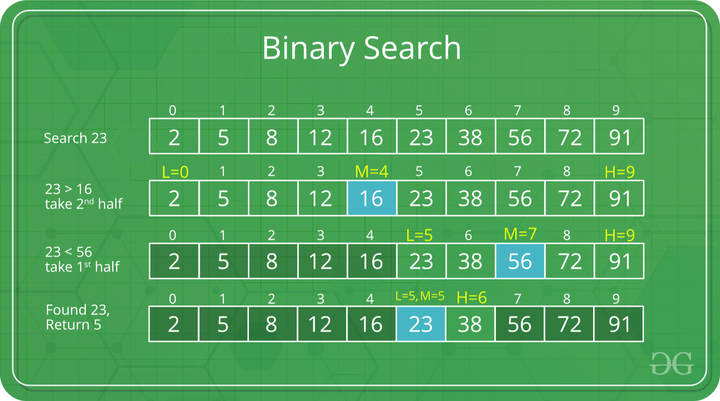
• Divide the data structure into 2 equal half to find the target
• Determine 3 indexes

    min = 0
    max = size
    mid = min + (max - min) /2
  

• Check the value mid position
  • if data[mid] == target -> found the target
  • if data[mid] > target means the target is in the lower part -> set max = mid - 1
  • if data[mid] < target means the target is in the upper part -> set min = mid + 1
  • if min > max -> can not find the target

Implementation

Iterative
TODO: Recursive

Code from github

public class BinarySearch {
  public static void main(String[] args) {
    int[] nums = new int[]{1,5,7,11,58,100,199,200,203};
    System.out.println(search(nums, 7));
  }
  private static int search(int[] nums, int searchValue) {
    int indexOfMax = nums.length - 1;
    int indexOfMin = 0;
    while (indexOfMax >= indexOfMin) {
      int indexOfMid = (indexOfMax + indexOfMin) / 2;
        if (nums[indexOfMid] == searchValue) {
            return indexOfMid;
        } else if (nums[indexOfMid] > searchValue) {
            indexOfMax = indexOfMid - 1;
        } else  {
            indexOfMin = indexOfMid + 1;
        }
    }
    return -1;
  }
}